com.supermap.data

类 TransformationMode

java.lang.Object

com.supermap.data.Enum

com.supermap.data.TransformationMode

public final class TransformationMode
extends Enum

该类定义了数据配准模式类型常量。

数据配准模式主要有四种：线性配准、矩形配准、二次多项式配准和偏移配准。

线性配准：也称仿射变换，这种配准方法假设地图因变形而引起的实际比例尺在 x 和 y 方向上都不相同，因此，具有图纸变形的纠正功能。假设 x、y 为输入图像的原始坐标，X、Y为纠正后的输出坐标，则坐标变换的公式如下：

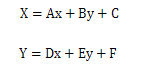
上式中6个待定系数A、B、C、D、E、F，可以通过选择配准图层和参考图层的同名控制点来确定。若需计算这6个待定系数，理论上至少需要获取不在同一直线上的3个控制点坐标。若取常数项系数 C、F 为0，则至少需要2个控制点，所以实际应用中，通常利用2个以上的点来进行几何纠正。这里待定系数是通过最小二乘法的原理进行求解的。线性变换是最常用的一种配准纠正方法，由于同时考虑了 x 和 y 方向上的变形，所以纠正后的坐标在不同的方向上的长度比会不同，表现为原始坐标会发生如缩放、旋转、平移、扭转等变化后得到输出坐标。

矩形配准：实质上是一种特殊的、有限定条件的线性配准。如果原始图像为规则矩形，配准纠正后的图像仍是规则矩形，则选择2个相对的角点就可以确定矩形4个角点的坐标，在线性配准的纠正公式中，常数项取作0，则已知4个角点坐标就可以求解得到纠正公式，从而实现几何纠正。由于只需要取2个相对的角点，因而既方便又节省时间，同时，也减少了由于选取多个控制点造成的误差累积。由于矩形配准未计算输出结果的误差，所以其配准精度不可知，是一种精度不高的粗纠正。

二次多项式配准：遥感中常用的精度较高的配准方法。多项式纠正把原始图像的变形看成是某种曲面，输出图像为规则平面。从理论上讲，任何曲面都能以适当高次的多项式来拟合。一般用二次多项式就可以对变形比较严重的图像进行纠正，并得到较高的精度。二次多项式的纠正公式如下：

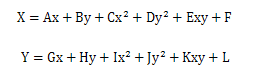
上式中共有12个待定系数，理论上，需要6个控制点就可实现几何纠正，但为了得到比较高的精度，一般要求二次多项式纠正的控制点至少为7个，适当增加控制点的个数，可以明显提高图形配准的精度。多项式待定系数是通过所选定的控制点坐标，按照最小二乘法回归来确定的。对比线性配准的纠正公式，可以得知，线性配准其实是一次多项式配准，二次多项式配准比线性配准需要更多的控制点，也会纠正更多的变形。对于多数具有中等几何变形的小区域的卫星图像，一次线性多项式就可以纠正6种几何变形。

偏移配准：偏移配准仅需要一组控制点和参考点，分别对 x 坐标和 y 坐标求差值，再利用差值对原数据集所有组坐标点进行偏移。

字段概要

字段

限定符和类型	字段和说明
static TransformationMode	LINEAR 线性配准。
static TransformationMode	OFFSET 偏移配准。
static TransformationMode	RECT 矩形配准。
static TransformationMode	SQUARE 二次多项式配准。

方法概要

从类继承的方法 com.supermap.data.Enum

equals, getEnums, getNameByValue, getNames, getPredefineValues, getValueByName, getValues, hashCode, isDefined, isDefined, name, parse, parse, toString, value

从类继承的方法 java.lang.Object

getClass, notify, notifyAll, wait, wait, wait

字段详细资料

RECT

public static final TransformationMode RECT

矩形配准。

LINEAR

public static final TransformationMode LINEAR

线性配准。

SQUARE

public static final TransformationMode SQUARE

二次多项式配准。

OFFSET

public static final TransformationMode OFFSET

偏移配准。