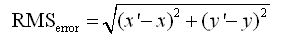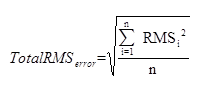During the procedure of registering, the application will calculate residual-X, residual-Y, root-mean-square error and total error (the sum of all root-mean-square errors) of all points.
A residual is the difference between the observed value and the estimated value. The observed points are control points in the reference layer which can be got either through clicking at the reference layer or entering coordinate-X, coordinate-Y. The estimated point is fitted by calculating all control points as some algorithm.
- Residual-X
The distance between the observation point and estimated point along the coordinate X.
- Residual-Y
The distance between the observation point and calculation point along the coordinate Y.
- Root-mean-square error
For the two algorithms Linear and Polynomial, the root mean square error formula will be used for calculating the error of each control point. Among the formula, x and y is the original coordinates and x’, y’ is the computed coordinates that are called estimation coordinate. The differences between the original coordinates and estimation coordinates represent the precision that each control points should be corrected.
Among the formula, x and y is the original coordinates and x’, y’ is the estimated coordinates that are called estimation coordinate. The differences between the original coordinates and estimation coordinates represent the precision that each control points should be corrected.
- Total root-mean-square error
The total root-mean-square error reflects an accumulation of errors when performing a registration. In general, the value is used for the calibration. The formula to get the value is:
Among them, n is the number of control points, and RMS is the RMSerror of every control point. The point whose RMSerror is bigger than the acceptable TotalRMSerror can be removed or adjusted.