程序集: SuperMap.Analyst.SpatialAnalyst (in SuperMap.Analyst.SpatialAnalyst)
版本: dll
 语法
语法
| C# |
|---|
public class InterpolationKrigingParameter : InterpolationParameter, IDisposable |
 备注
备注
Kriging 法为地质统计学上一种空间资料内插处理方法,主要的目的是利用各数据点间变异数 (variance) 的大小来推求某一未知点与各已知点的权重关系,再由各数据点的值和其与未知点的权重关系推求未知点的值。Kriging 法最大的特色不仅是提供一个最小估计误差的预测值,并且可明确的指出误差值的大小。一般而言,许多地质参数,如地形面本身即具有连续的性质,故在一短距离内的任两点必有空间上的关系。反之,在一不规则面上的两点若相距甚远,则在统计意义上可视为互为独立(stastically indepedent),这种随距离而改变的空间上连续性,可用半变异图 (semivariogram) 来表现。因此,若想由已知的散乱点来推求某一未知点的值,则可利用半变异图推求各已知点及欲求值点的空间关系。再由此空间参数推求半变异数,由各数据点间的半变异数可推求未知点与已知点间的权重关系,进而推求出未知点的值。
克吕金法的优点是以空间统计学作为其坚实的理论基础。物理含义明确;不但能估计测定参数的空间变异分布,而且还可以估算参数的方差分布。克吕金法的缺点是计算步骤较烦琐,计算量大,且变异函数有时需要根据经验人为选定。
克吕金插值法可以采用两种方式来获取参与插值的采样点,进而获得相应位置点的预测值,一个是在待计算预测值位置点周围一定范围内,获取该范围内的所有采样点,通过特定的插值计算公式获得该位置点的预测值;另一个是在待计算预测值位置点周围获取一定数目的采样点,通过特定的插值计算公式获得该位置点的预测值。
克吕金插值过程是一个多步骤的处理过程,包括:
1. 创建变异图和协方差函数来估计统计相关(也称为空间自相关)的值;
2. 预测待计算位置点的未知值。
半变异函数与半变异图:
计算所有采样点中相距 h 个单位的任意两点的半变异函数值,那么任意两点的距离h一般是唯一的,将所有的点对的距离与相应的半变函数值快速显示在以 h 为 X 坐标轴和以半变函数值为Y坐标轴的坐标空间内,就得到了半变异图。相距距离愈小的点其半变异数愈小,而随着距离的增加,任两点间的空间相依关系愈小,使得半变异函数值趋向于一稳定值。此稳定值我们称之为基台值(Sill);而达到基台值时的最小h 值称之为自相关阈值(Range)。
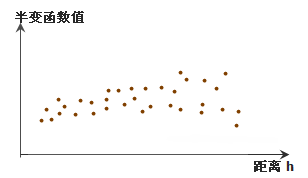
某半变异图
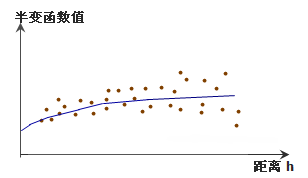
某半变异函数拟合曲线图

有关概念示意图
块金效应:
当点间距离为 0(比如,步长=0)时,半变函数值为 0。然而,在一个无限小的距离内,半变函数通常显示出块金效应,这是一个大于 0 的值。如果半变函数在Y周上的截距式 2 ,则块金效应值为 2。
块金效应属于测量误差,或者是小于采样步长的小距离上的空间变化,或者两者兼而有之。测量误差主要是由于观测仪器的内在误差引起的。自然现象的空间变异范围很大(可以在很小的尺度上,也可以在很大的尺度上)。小于步长尺度上的变化就表现为块金的一部分。
半变异图的获得是进行空间插值预测的关键步骤之一,克吕金法的主要应用之一就是预测非采样点的属性值,半变异图提供了采样点的空间自相关信息,根据半变异图,选择合适的半变异模型,即拟合半变异图的曲线模型。
不同的模型将会影响所获得的预测结果,如果接近原点处的半变异函数曲线越陡,则较近领域对该预测值的影响就越大。因此输出表面就会越不光滑。
SuperMap 支持的半变函数模型有指数型、球型和高斯型。详细信息参见 VariogramMode 类。
完成模型的确定后,就可以使用选定的模型,对采样点数据进行插值分析了。
 示例
示例
以下代码示范了根据给定的点数据集、用于插值的字段和目标数据源进行插值分析,并且选择克吕金插值法进行插值。
public void InterpolationKriging(DatasetVector datasetPoints, String zFieldName, Datasource targetDatasource) { //获得一个合法的名称作为结果数据集的的名称 String resultDatasetName = targetDatasource.Datasets.GetAvailableDatasetName("resultDatasetGrid"); //设置克吕金内插法参数 InterpolationKrigingParameter interpolationMethodKrigingParam = new InterpolationKrigingParameter(); interpolationMethodKrigingParam.ExpectedCount = 5; interpolationMethodKrigingParam.Bounds = datasetPoints.Bounds; interpolationMethodKrigingParam.Resolution = 285; interpolationMethodKrigingParam.SearchMode = SearchMode.KdTreeFixedCount; interpolationMethodKrigingParam.VariogramMode = VariogramMode.Exponential; //调用插值分析类的插值分析方法实现对点数据集的插值,并获得分析结果 DatasetGrid resultInterpolationGrid = Interpolator.Interpolate(interpolationMethodKrigingParam, datasetPoints, zFieldName, 0.7, targetDatasource, resultDatasetName, PixelFormat.Single); }
 继承层次
继承层次
SuperMap.Analyst.SpatialAnalyst..::.InterpolationParameter
SuperMap.Analyst.SpatialAnalyst..::.InterpolationKrigingParameter