| 地理数据坐标系转换 |
在进行地理数据处理的工作中，坐标系转换问题会经常遇到。当前最便捷的定位方法就是GPS卫星定位，GPS定位的数据是基于WGS84坐标系上的数据，而各国家采用的往往是早先建立的国家坐标系，为了避免出现矛盾，就需要将WGS84定位数据转换到国家坐标系上，也就是进行坐标系（参照系）的转换。
在进行坐标系变换方法的讲解前，首先需要清楚以下两种坐标系的概念：
l 大地经纬度坐标系——大地测量中以参考椭球面为基准面的坐标。地面点P的位置用大地经度ϕ、大地纬度λ和大地高h表示。当点在参考椭球面上时，仅用大地经度和大地纬度表示。大地经度是通过该点的大地子午面与起始大地子午面之间的夹角，大地纬度是通过该点的法线与赤道面的夹角，大地高是地面点沿法线到参考椭球面的距离。
l 空间直角坐标系——基于地心的直角坐标系，用X、Y、Z表示，其中直角坐标系的原点位于地心；Z轴与地球旋转轴重合（极轴），向北为正方向；X轴穿过本初子午线与赤道的交点，向东为正方向；Y轴穿过赤道与东经90º的交点。
在实际应用中，我们通常需要将某参照系下的经纬度数据转换到新参照系下的经纬度数据，这种坐标变换的基本步骤为：将原经纬度坐标变换为空间直角坐标，再将变换后的原空间直角坐标通过指定的转换方法（三参数转换法或七参数转换法）转换为目标空间直角坐标，最后将目标空间直角坐标变换为经纬度坐标，从而完成不同参照系下经纬度坐标的相互转换。
从经纬度坐标变换为空间直角坐标以及从空间直角坐标变换为经纬度坐标都是基于标准的变换公式完成的，这里不做重点叙述。下面主要详细介绍坐标系转换方法，目前主要使用两大类转换方法：三参数转换法、七参数转换法。
三参数转换（EPSG坐标运算方法9603）：
三参数转换法是假设原坐标的参考椭球体与目标坐标的参考椭球体的长、短轴相互平行，零经线为格林威治本初子午线，从原坐标系转换到目标坐标系的三平移参数为dX、dY、dZ，那么转换基本原理为：
其中，
、
、
为原空间直角坐标；
、
、
为目标空间直角坐标（这里需要进行大地经纬度坐标与空间直角坐标的相互转换）。因此，只要知道原坐标系与目标坐标系的dX、dY、dZ三个偏移参数，即可完成坐标系的变换；一般情况下需要通过实测数据去拟合获得dX、dY、dZ三个偏移参数。
简化莫洛金斯基转换：
莫洛金斯基推出的转换公式，可以将上述的三参数转换方法的计算步骤合二为一，即大地经纬度坐标与空间直角坐标的转换同空间直角坐标系间的转换结合起来，这种简化后的形式非常适合三参数坐标系的转换。
七参数转换：
三参数转换法的假设条件通常是不成立的，对于一个国家或地域的局部地区来说，该假设所引起的误差可以忽略，一般小于数据的观测精度。然而，当精度要求较高时，三参数转换法既不适合在全球范围应用，也不适合地域广大的国家与地区应用。因此，目前采用精度较高的七参数法。
从一个大地经纬度坐标系变换到另一个大地经纬度坐标系一般需要经过三个环节：大地经纬度坐标系到空间直角坐标系>空间直角坐标系到空间直角坐标系>空间直角坐标系到大地经纬度坐标系。其中的中间环节，空间直角坐标到空间直角坐标采用七参数赫尔默特（Helmert）转换法，其转换矩阵为著名的布尔沙-沃尔夫（Bursa-Wolf）公式：
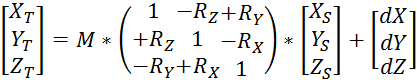
式中，（
）为原空间直角坐标系中的点坐标，（
）为目标空间直角坐标系中的点坐标；其他均为转换参数。
转换参数的定义不唯一，可引伸出不同的转换方法。国际大地测量协会（IAG）通过ISO19111建议采用以下参数定义（“位置矢量转换方法”）：
（dX,dY,dZ）:两坐标系的原点平移矢量（平移参数），原坐标系中的点位置矢量加上原点平移矢量即得到该点在目标坐标系中的位置矢量。平移参数也就是原坐标系的原点在目标坐标系中的坐标值。
（
,
,
）：位置矢量的旋转角（旋转参数）。参数符号约定如下：从直角坐标系原点，沿轴正向看，位置矢量绕轴顺时针旋转为正。从原坐标系到目标坐标系，如果绕Z轴的旋转角度为正，那么转换后坐标点的经度将增大。
M：位置矢量的比例因子（尺度比参数），位置矢量从原坐标系到目标坐标系的尺度伸缩量。
，其中dS为尺度校正量，以百万分之一计（ppm）。
由于七参数赫尔默特（Helmert）转换法的三个旋转参数有两种相反的符号协定，EPSG（欧洲石油勘探组织）将其分为两种不同的转换方法，其一称位置矢量法，也成为布尔沙-沃尔夫（Bursa-Wolf）转换法；另一种称为坐标框架法。
位置矢量法与坐标框架法的区别在于旋转参数的约定上，坐标框架法的转换公式为：
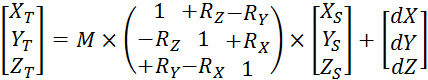
（dX,dY,dZ）与M参数的定义与位置矢量法相同，不同在于（,,）三个旋转参数的符号的约定：从直角坐标系原点，沿轴正向看，坐标参考框架绕轴顺时针旋转为正。从原坐标系转换到目标坐标系，如果绕Z轴的旋转角度为正，那么转换后坐标点的经度将变小。
如果不考虑旋转因素，位置矢量法和坐标框架法是一致的。需要注意的是，同样的旋转变换，第一种方法中的转换参数为正，二者在第二种方法中却是负的。所以，在基准面转换前，必须明确旋转参数的符号约定，可以说，参数的符号是与坐标系转换方法相关联的。